Surface is a basic component of any Optical Element. Some set of Elements defined within Application contains single surface.
It is a default type of new surface.
You can either create new Spherical Surface or redefine any existing Single-Surface Optical Element.
To create new Plane Surface:
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
Spherical Surface is surface of revolution that is defined analytically according to following equation:
![]()
where R -- radius of curvature at top point of Surface.
You can either create new Spherical Surface or redefine any existing Single-Surface Optical Element.
To create new Spherical Surface:
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
After Spherical Surface has bee defined, you can set parameters of Spherical Surface such as radius of curvature and Clear aperture. It can be provided through Shape group within hierarchical structure of Surface:
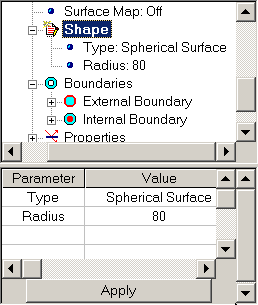
To set parameters of Spherical Surface:
You can change form-factor of any Element redefining parameters responsible for its shape. Corresponding parameters are combined into Shape group of properties of hierarchical tree graph of Element.
To change form factor of Element’s shape:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
Cylindrical surface within Application is a part of cylindrical skin restricted with trimmed curve that is found because of projection of external and internal boundaries of Clear Aperture onto cylinder as it shown on figure below:
Origin of internal Coordinate system of the Cylindrical Surface is placed on the surface at the geometry center of External boundaries of Clear Aperture (while eccentricity is set to zero). Figures below illustrate examples of Cylindrical Surface:
|
|
|
|
Surface restricted with external ellipse and internal circle without eccentricity |
Surface restricted with external and internal rectangle with eccentricity |
You can either create new Spherical Surface or redefine any existing Single-Surface Optical Element.
To create new Cylindrical Surface:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
Quadric Surface is surface of revolution that is defined analytically according to following equation:
![]()
where R - radius of curvature at top point of Surface; e2 - squared eccentricity of Surface.
You can either create new Quadric Surface or redefine any existing Single-Surface Optical Element.
To create new Quadric Surface:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
After Quadric Surface has been created, you can edit its parameters to define desired surface shape. It can be provided through Shape group within hierarchical structure of Surface:
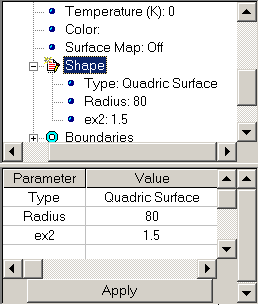
Note if real solution of surface equation cannot be found for assigned parameter combination, then there is no corresponding surface of revolution. In this case, the surface is excluded from both system and layout.
If External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
Parabolic Surface is a special case of Quadric Surface with squared eccentricity coefficient ex2 equal to unit value (1). See Quadric Surface for reference.
Aspherical First Surface is surface of revolution that is defined analytically according to following equation:
![]()
where R - radius of curvature at top point of Surface; A1=-2R - first Aspherical coefficient; Ai - Aspherical coefficients of higher orders.
You can either create new Aspherical First Surface or redefine any existing Single-Surface Optical Element.
To create new Aspherical First Surface:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
After Aspherical First Surface has been created, you can edit its parameters to define desired surface shape. It can be provided through Shape group within hierarchical structure of Surface:
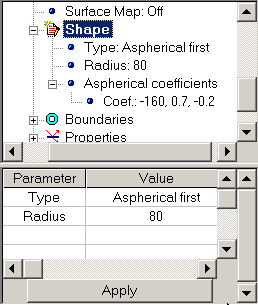
To define values of aspherical coefficient:
Note if real solution of surface equation cannot be found for assigned parameter combination, then there is no corresponding surface of revolution. In this case, the surface is excluded from both system and layout.
If External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
Aspherical Second Surface is surface of revolution that is defined analytically according to following equation:
![]()
where R - radius of curvature at top point of Surface; B1=??? - first Aspherical coefficient; Bi - Aspherical coefficients of higher orders.
You can either create new Aspherical Second Surface or redefine any existing Single-Surface Optical Element.
To create new Aspherical Second Surface:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
After Quadric Surface has been created, you can edit its parameters to define desired surface shape. Following parameters are available for editing: radius of curvature at top point of surface and square of eccentricity.
If there is no real solution for assigned parameter combination, then there is no corresponding surface of revolution. In this case, the surface is excluded from both system and layout.
Aspherical International Surface is surface of revolution that is defined analytically according to following equation:
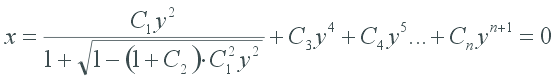
where C1=??? - first Aspherical coefficient; Ci - Aspherical coefficients of higher orders.
You can either create new International Aspheric Surface or redefine any existing Single-Surface Optical Element.
To create new Aspherical Second Surface:
Note if External Boundaries of Clear Aperture will exceed double size of Radius value, some undesirable effects may occur during visualization.
To redefine existing single-surface Optical Element:
Note you can redefine just single-surface Element.
To redefine surface within complex Optical Element:
After Quadric Surface has been created, you can edit its parameters to define desired surface shape. Following parameters are available for editing: radius of curvature at top point of surface and square of eccentricity.
If there is no real solution for assigned parameter combination, then there is no corresponding surface of revolution. In this case, the surface is excluded from both system and layout.
All reflectors are considered as a Single-Surface Element.
Application provides defining concave and convex reflectors of some typical configurations.
Pyramidal Reflector is the Optical Element representing truncated or non-truncated pyramid without cowers. Regular polygon is used as the base of pyramid. Origin of internal coordinate system of the element locates at the center of pyramid base, while OX axis being perpendicular to the base.
Below there are examples of pyramidal reflector:
|
|
|
|
Non-truncated pyramidal reflector |
Truncated pyramidal reflector |
General set of parameters of Pyramidal Reflectors is the same as for any other Element. You can set location and orientation of Pyramidal reflector, define optical and thermo properties of reflector’s surface, set visibility options and so on.
To create new Pyramidal Reflector:
Parameters available for editing are illustrated with figure below:
|
|
|
Note it is allowable to set Radius and/or Length values as negative. In this case, paired Pyramidal Reflector will appear. Example of such kind of Reflector is shown below:
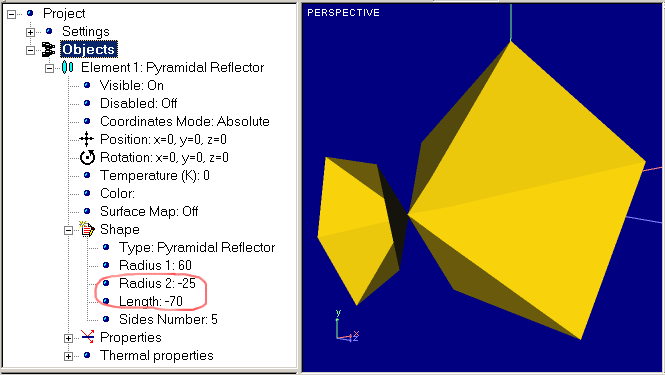
Pyramidal Rectangle Reflector is special type of Pyramidal Reflector with rectangular base. Below there is example of defining shape and location of pyramidal rectangular reflector. While just regular quadrangle (square polygon) may be used as a base of Pyramidal Reflector, you can set arbitrary parameters of rectangle used as a base for Pyramidal Rectangle Reflector as it shown below:
|
|
|
|
Pyramidal Reflector |
Pyramidal Rectangle Reflector |
Note different initial orientation of both types of Pyramidal Reflectors.
|
|
|
To get non-truncated Pyramidal Rectangle Reflector you should set value of any H parameters to zero.
Note it is allowable to set Radius and/or Length values as negative. In this case, paired Pyramidal Rectangle Reflector will appear. Examples of such kind of Reflector are shown below:
|
|
|
|
Non-truncated Pyramidal Rectangle Reflector |
Paired Pyramidal Rectangle Reflector |
Axial Cone is the Optical Element representing truncated or non-truncated conical surface of rotation without cowers. As a default, origin of internal coordinate system of the element locates at the center of cone base, while OX axis is axis of rotation.
Below there are examples of pyramidal reflector:
|
|
|
|
Non-truncated pyramidal reflector |
Truncated pyramidal reflector |
General set of parameters of Axial Cone is the same as for any other Element. You can set location and orientation of Axial Cone, define optical and thermo properties of reflector’s surface, set visibility options and so on.
To create new Axial Cone Reflector:
You can change form-factor of your Axial Cone. Corresponding parameters are combined into Shape group of properties of hierarchical tree graph of Element.
Parameters available for editing are illustrated with figure below:
|
x1 – Coordinate of Axial Cone’s first base along 0X-axis. h1 – Half-side (radius) of first cone base. x2 – Coordinate of Axial Cone’s second base along 0X-axis. h2 – Half-side (radius) of second cone base. |
Note negative values of h1 and h2 will be converted to positive ones automatically.
Some surfaces defined within Application have transversal section shape forming different kind of cycloidal curves. That’s why some general consideration may be useful.
Generally, cycloidal curves appear because of rotation of circles one around another. While smaller circle rotate around external part of bigger circle we will get epicycloidal curve. Otherwise, hypocycloidal curve will appear.
Procedure of building cycloid is standard and common for all variety of ones.
|
|
|
The parametric epicycloid equations used in Application are being as follows:
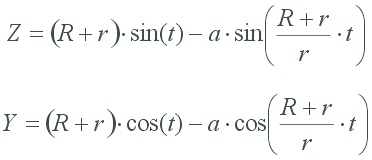
Depending on r value and different correlation between r and a values all available types of cycloidal curves can be reached:
|
|
Type of curve |
a=r |
a<r |
a>r |
|
r>0 |
Epicycloid |
|
|
|
|
Normal epicycloid |
Shortened epicycloid |
Enlarged epicycloid |
||
| r<0 |
Hypocycloid |
|
|
|
|
Normal hypocycloid |
Shortened hypocycloid |
Enlarged hypocycloid |
||
Cycloidal Quadric Reflector is a special type of surface. Each transversal section of such kind of surface is cycloidal curve while axial longitudinal section is parabolic curve. Radius of stationary circle R in each cross-section is obtained from definition of paraboloidal surface of revolution as function of its X-coordinate. Local coordinate system of the element locates at the top surface point, while that 0X axis is the axis of rotation of the basic quadric surface. Cycloidal Quadric Reflector is inscribed into Parabolic Surfaces with the same parameters of curvature radius of top surface point and eccentricity coefficient.
Below there are examples of paraboloidal cycloidal reflector:
|
|
|
|
Epicycloidal Quadric Reflector |
Hypocycloidal Quadric Reflector |
To create new Cycloidal Quadric Reflector:
Parameters available for editing are illustrated with figure below:
|
|
Note R, r, and a parameters does not define cycloidal curve directly because they are not constant. That’s why, in fact, you are defining two ratios:
|
If no real surface can be defined with assigned parameter combination, surface will be excluded from layout of 3D Viewer.
Cycloidal Parabolic Reflector is special case of Cycloidal Quadric Reflector with squared eccentricity coefficient Ex2 equal to unit value (1). See Cycloidal Quadric Reflector for reference.
Cycloidal Conic Reflector is a special type of surface. Each transversal section of such kind of surface is cycloidal curve built on the base of conical surface of revolution. Correspondingly, radius of stationary circle R in each cross-section is defined with cone equation. Origin of internal coordinate system (Pivot Point) of the element locates at the geometrical center of cone base, while 0X axis is the axis of rotation of the basic conical surface.
Below there are examples of paraboloidal cycloidal reflector:
|
|
|
|
Epicycloidal Cone Reflector |
Hypocycloidal Cone Reflector |
To create new Cycloidal Cone Reflector:
Parameters available for editing are illustrated with figure below:
|
|
Note length of reflector is sign-depended value affecting orientation of Cycloidal Cone Reflector. |
In contrary to Cycloidal Quadric Reflectors, you are not able to create truncated Cycloidal Cone Reflector.
If no real surface can be defined with assigned parameter combination, surface will be excluded from layout of 3D Viewer.
There are several types of pipe-like guides integrated into Application. It can be produced with cylindrical cycloidal or cycloidal surface, or composed with periodically repeated figures.
You can add a slit for radiance output in the in the direction of negative values of Y-axis. The length of the slit is always equal to the length of guide and its width is assigned as central angle relative to cylinder axis. Two half-planes intersecting at the cylinder axis bound the slit, which is called also “Gap”.
Simple Cylindrical Guide is an element consisting of reflective cylindrical surface. Guide can be equipped with a slit for radiance output placed at the bottom part of Guide (as a default). Pivot Point (origin of the internal coordinate system) of the Cylindrical Guide locates at the center of the first cylinder base, at that OX axis is the axis of cylinder.
|
|
|
|
Cylindrical guide with slit |
Cylindrical Guide without slit rotated around 0X-axis |
To create new Cylinder Guide:
You can change form-factor of your Cylinder Guide. See Form Factor for reference. Parameters available for editing are illustrated with figure below:
|
|
|
Cycloidal Guide is an element consisting of reflective surface having cycloidal section along whole length of guide. All types of cycloids can be used. Guide can be equipped with a slit for radiance output placed at the bottom part of Guide (as a default). Pivot Point (origin of the internal coordinate system) of the Cylindrical Guide locates at the center of the first cylinder base, at that OX axis is the axis of cylinder.
At the figure below, examples of both epicycloidal and hypocycloidal guides are shown:
|
|
|
|
Shortened Epicycloidal Guide with slit |
Enlarged Hypocycloidal Guide without slit |
To create new Cycloidal Guide:
You can change form-factor of your Cycloidal Guide. See Form-Factor for reference. Parameters available for editing are illustrated with figure below:
|
|
|
Note combining different values of R, r, and a parameters, you are able to get enough complex shapes of Cycloidal Guides. Some examples are shown below:
|
|
|
|
Shortened Epicycloidal Guide |
Enlarged Hypocycloidal Guide |
Note both guides shown above have the same shape parameters except first of them is epicycloidal guide and second is hypocycloidal one.
Prismatic Guide is an element consisting of complicated cylindrical surface having non-zero thickness. Although it considered as single-surface Element it contain Optical Material. Either outer or inner surface of Prismatic guide Element has array of triangle prisms forming periodical structure. Guide can be equipped with a slit for radiance output. Origin of the internal coordinate system of the element locates at the center of the first cylinder base, at that OX axis is the axis of cylinder.
|
|
|
|
External prismatic guide with slit |
Internal prismatic guide without slit |
To create new Prismatic Guide:
Note you can redefine just single-surface Element. You can also redefine any surface belonging complex Optical Element but it is not recommended.
Parameters dealing with form-factor of Prismatic guide are combined into Shape group of properties of hierarchical tree graph of Element and shown below. To change shape of your Guide See Form-Factor for reference.
|
|
|
Note zero value of “Prism height” transforms prismatic guide into true pipe with the wall thickness equal to “Base thickness”.
Some combinations of positive and negative values are supported. This permits to get prismatic structure, directed inside element towards cylinder axis.
Sawtooth Guide is a more general type of Prismatic Guide with array of arbitrary profile prisms forming periodical structure either onto external or internal guide surface. Origin of the internal coordinate system of the element locates at the center of the first cylinder base, at that OX axis is the axis of cylinder.
There is a slit for radiance output in the bottom part cylinder (more exactly, in the direction of negative values of Y). The length of the slit is always equal to the length of cylinder and its width is assigned as central angle relative to cylinder axis. Two half-planes intersecting at the cylinder axis bound the slit, which is called also “Gap”.
|
|
|
|
External prismatic sawtooth guide without slit |
Internal prismatic sawtooth guide with slit |
To create new Sawtooth Guide:
Note no Element can be redefined to get Sawtooth Guide.
Parameters dealing with form-factor of Prismatic guide are combined into Shape group of properties of hierarchical tree graph of Element. Note there is one more subgroup, Height Array to define profile of Guide
|
Shape |
|
|
|
Height Array subgroup |
|
|
Height Array – table, which defines the prism profile. At the “Value” column the difference between radius “Rt” of the current surface point and radius R1 is assigned as function of partial arc length “t”: (Rt-R1) = F(t)
The arc length “t” is obtained as:
![]()
where t -– current arc length; dt – step value i.e. arc increment, dt=T/(N-1); T – arc length equal to period of structure; K – number of the current surface point; N – total number of surface points in the table (number of points in structure period defining surface profile).
Currently, the arc T, representing period of structure, is always divided into equal parts, depending upon the number of values assigned in the table by user. The said number and arc increment dt entailed are defined automatically under pressing “Apply” button.
Fiber Guide is flexible optical element used to provide light feeding to desired point of Optical Scheme. Within Application, Fiber Guide is considered as multi-fiber light guide with regularly packed into cylindrical loop. Pivot Point (origin of the internal coordinate system) is placed at the geometrical center of the entrance side of Fiber Guide. Example of Fiber Guide is shown below:
|
|
|
Fiber Guide |
Note Fiber Guide is depicted with entrance and exit active face. External boundaries are not shown (white curves imitating envelope of fiber guide are added just to denote possible guide pass) and actual end-to-end ray tracing is nod kept.
To create new Fiber Guide:
Note Thermal Properties fill affect entrance and exit active faces only due to absence of finite-model of external envelope.
You can change some parameters affecting form-factor of your Fiber Guide. See Form Factor for reference. Parameters available for editing are illustrated with figure below:
|
|
H – Radius of Clear Aperture of Fiber Guide. Exit position x; Exit position y; Exit position z – Position of exit face with respect to entrance one. Exit rotation x; Exit rotation y; Exit rotation z – Angle values defining orientation of exit face with respect to axes of internal coordinate system of exit face of Fiber Guide. Center of rotation is noted with the red point. See Polar Coordinate System for reference |
Note you cannot change type of Clear Aperture of Fiber Guide; to do it you will have to use additional Optical Element like diaphragm.
Lattices integrated into Application are special Optical Element. Surface of that Elements consist of infinitely thin ribbons. Lattices are considered as single complex surface.
Several types of Lattices are defined within Application: Lattice Plane is a round plane (with optional round hole at the center part), Lattice Cylinders representing cylindrical lattice, Lattice Quadric representing quadric lattice surface, and Lattice representing combination of Lattice Cylinder and Lattice Spherical Surface. All type of Lattices may be represented as Hexagonal and Rectangular ones. To create Lattices you should use Lattice chapter at Element item of Insert Menu or Insert New Element item of context menu of Project docked window.
General set of parameters of Lattices is the same as for any other Element. You can set location and orientation of Lattice, define optical and thermo properties of lattice’s material, set visibility options and so on.
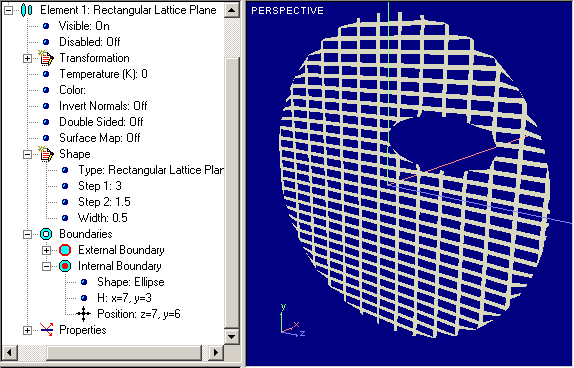
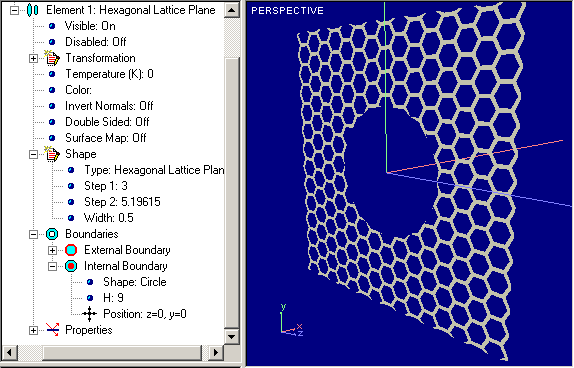
That is lattice variant of Plane Surface. Examples of Lattice Cylinders are shown below:
 |
 |
|
Rectangular Lattice Plane |
Hexagonal Lattice Plane |
Origin of internal Coordinate System is at the geometrical center of Lattice Plane.
To create Lattice Plane:
You can change form-factor of your Lattice. See Form Factor for reference. Parameters available for editing shown below are combined into Shape group of properties of hierarchical tree graph of Element and shown below:
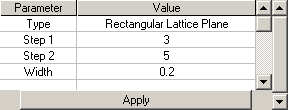 |
|
To change structure of Lattice Plane surface:
That is lattice variant of Cylindrical Guide except fact that there is no special slit for radiance output. Examples of Lattice Cylinders are shown below:
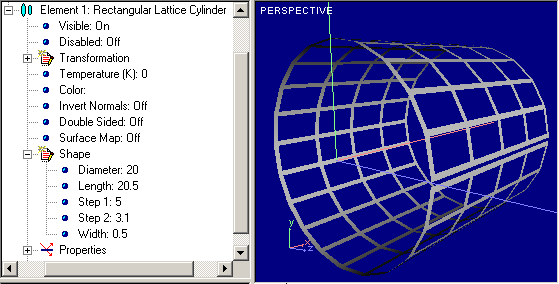 |
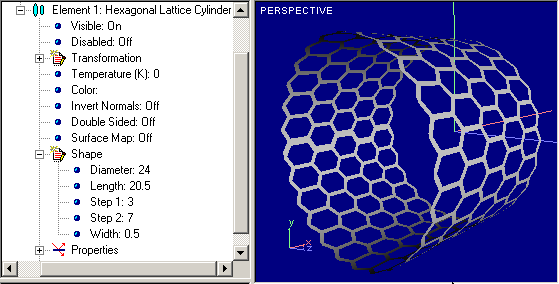 |
|
Rectangular Lattice Cylinder |
Hexagonal Lattice Cylinder |
To create Lattice Cylinder:
You can change form-factor of your Lattice. See Form Factor for reference. Parameters available for editing shown below are combined into Shape group of properties of hierarchical tree graph of Element and shown below:
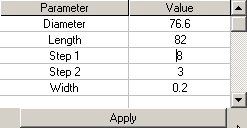 |
|
As you can see, set of parameters looks like combination of reduced parameter set of Cylindrical Guide and parameters that is specific for lattices.
To change structure of Lattice Cylinder surface:
Note in the case combination of Diameter, Step 2, and Width parameters cannot provide integer number of lattice cells to close cylinder it will have slit as it shown on figures above.
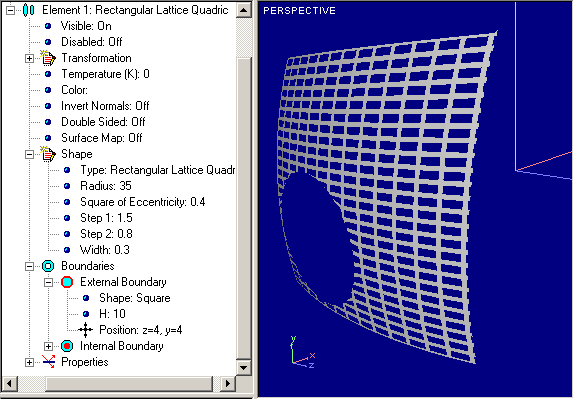
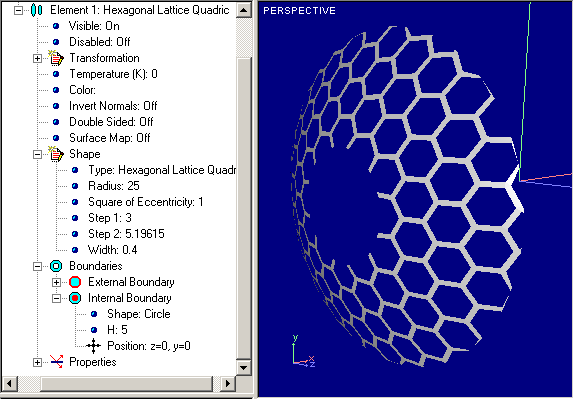
That is a lattice variant of Quadric Surface except fact that there is no special slit for radiance output. Examples of Lattice Cylinders are shown below:
 |
 |
|
Rectangular Lattice Quadric |
Hexagonal Lattice Quadric |
Note origin of internal Coordinate System is placed on the axis of quadric surface but at the plane consisting outer borders of Element (in contrary to usual Quadric Surface having it at the top surface point). It is to provide more easy combination of Lattice Quadric with other Lattice Elements (like Lattice Cylinder).
To create Lattice Quadric surface:
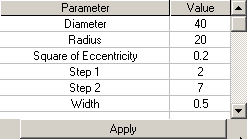
You can change form-factor of your Lattice. See Form Factor for reference. Parameters available for editing shown below are combined into Shape group of properties of hierarchical tree graph of Element and shown below:
 |
|
As you can see, set of parameters looks like combination of parameters of Quadric Surface and parameters that is specific for lattices.
To change structure of Lattice Quadric surface:
Lattice Frames are special type of geometrical objects representing cylinder opened from one side and having spherical cover on the other side and having lattice surface. Origin of internal Coordinate system of the element is placed on the opened side of the cylinder, while OX axis is the cylinder axis. Examples of Lattice Frames are shown below:
|
|
|
|
Rectangular Lattice Frame |
Hexagonal Lattice Frame |
To create Lattice Frame:
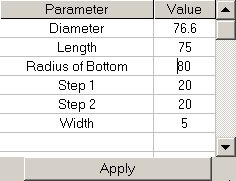
You can change form-factor of your Lattice. See Form Factor for reference. Parameters available for editing shown below are combined into Shape group of properties of hierarchical tree graph of Element and shown below:
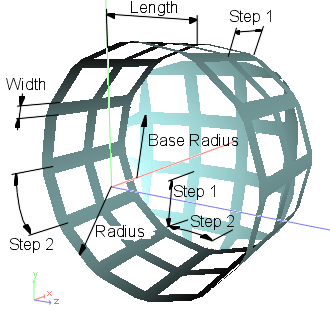
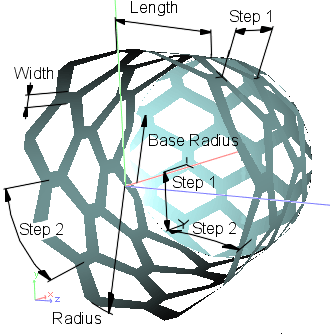
|
|
To change structure of Lattice frame surface:
Note in the case combination of Diameter, Step 2, and Width parameters cannot provide integer number of lattice cells to close cylinder it will have slit as it shown on figures above.
Triangular mesh is used to substitute current analytical surface by its finite-element triangular model. After substitution, all information about analytical representation of surface will be lost. You will able just rescale your surface along principal axes of Global Coordinate System. Note you are not able to redefine triangular mesh back to it analytical representation. In this case, new analytical surface will be created with default values of parameters. You will have to define all parameters anew.